Číselné soustavy používané pro zobrazování v počítači patří mezi soustavy poziční, tj. desítková hodnota každé číslice (znaku) závisí na její pozici vzhledem k řádové čárce.
Váhy v jednotlivých pozicích jsou mocniny základu soustavy.
U desítkové soustavy jsou to mocniny 10
u dvojkové soustavy mocniny 2
u hexadecimální mocniny 16
Desítkové číslo 725 lze tedy rozložit takto:
7*102+2*101+5*100
Podobně postupujeme u čísel vyjádřených ve dvojkové nebo šestnáctkové soustavě, (nebo kterékoliv jiné soustavě) chceme-li zjistit jejich desítkový ekvivalent.
Mocniny základu dvojkové soustavy
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 210 | atd. |
| 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | atd |
Příklady:
Převod z dvojkové do desítkové soustavy
01010111(2) = 1*26 +0*25 +1*24 +0*23 +1*22 +1*21 +1*20 =87(10)
Převod z šestnáctkové do desítkové soustavy
B5(16) = 11*161 +5*160 = 181(10)
U opačných převodů z desítkové soustavy do jiné musíme zjistit, která nejvyšší mocnina základu té soustavy, do níž převádíme, je v desítkovém čísle obsažena, eventuelně kolikrát, jde-li o soustavy s vyšším základem než 2.
Pak je třeba zapsat v příslušné pozici zbytek po odečtení mocniny od převáděného čísla (či po odečtení násobku mocniny)a celý postup opakovat pro výsledek (rozdíl).
Obvykle se používá mechanický postup dělení čísla základem soustavy a zaznamenávání zbytků (u hexadecimální soustavy můžeme dostat možné hodnoty u zbytku 1 – 15, nebo-li 1 – F).
Zbytky zapisujeme od konce, tj. od nejnižšího řádu výsledné převedené hodnoty.
Dílčí výsledky opět dělíme základem soustavy a výsledek posledního dělení je číslice (příp. znak) nejvyššího řádu. Dílčí výsledky opět dělíme základem soustavy a výsledek posledního dělení je číslice (příp. znak) nejvyššího řádu.

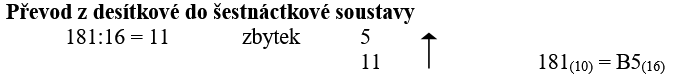
Všimněte si, že pro záznam třímístného desítkového čísla 181 stačí dva hexadecimální znaky, z nichž každý se převede na čtveřici bitů.

Čtveřice bitů (16 kombinací) a jejich odpovídající desítková hodnota (tučně)
dvouciferná čísla nahrazena písmenem , využito v hexadecimální soustavě, 1 čtveřice bitů = 1 šestnáctkový znak, tak se využije všech 16 možností
do 3 bytů, ve kterých je uložena mantisa (při uložení v pohyblivé řádové čárce), se tak „vejde“ větší číslo – až 7 desítkových číslic (=6 hexadecimálních znaků) = tzv. jednoduchá přesnost
písmena představují též desítkovou hodnotu
0000 0 0100 4 1000 8 1100 12 =C
0001 1 0101 5 1001 9 1101 13 =D
0010 2 0110 6 1010 10 =A 1110 14 =E
0011 3 0111 7 1011 11 =B 1111 15 =F