Zpřístupňuji zde svou seminární práci na téma návrhu konečného automatu.
Rubrika: Číselné systémy
Čítač – konkrétní příklad
Dnes bych se rád podělil o svou seminární práci na téma čítač, kterou jsem zpracoval ve 2. ročníku studia na SPŠ. Krom řešení konkrétního příkladu návrhu se pojednává o jednotlivých typech čítačů a něco málo potřebné teorie se tam také najde.
Číselné systémy
- Při převodu do binární či hexadecimální soustavy se užívá mocnin
- V každé soustavě je nejvyšší číslo o jednu menší než její základ
- U hexadecimální se chybějící bity ( čísla ) doplňují písmeny
| decimální | hexadecimální | octal | pětková | binární |
| 0 | 0 0 | 0 0 | 0 0 | 0 0 0 0 0 |
| 1 | 1 | 1 | 1 | 0 0 0 0 1 |
| 2 | 2 | 2 | 2 | 0 0 0 1 0 |
| 3 | 3 | 3 | 3 | 0 0 0 1 1 |
| 4 | 4 | 4 | 4 | 0 0 1 0 0 |
| 5 | 5 | 5 | 1 0 | 0 0 1 0 1 |
| 6 | 6 | 6 | 1 1 | 0 0 1 1 0 |
| 7 | 7 | 7 | 1 2 | 0 0 1 1 1 |
| 8 | 8 | 1 0 | 1 3 | 0 1 0 0 0 |
| 9 | 9 | 1 1 | 1 4 | 0 1 0 0 1 |
| 10 | A | 1 2 | 2 0 | 0 1 0 1 0 |
| 11 | B | 1 3 | 21 | 0 1 0 1 1 |
| 12 | C | 1 4 | 2 2 | 0 1 1 0 0 |
| 13 | D | 1 5 | 2 3 | 0 1 1 0 1 |
| 14 | E | 1 6 | 2 4 | 0 1 1 1 0 |
| 15 | F | 1 7 | 3 0 | 0 1 1 1 1 |
| 16 | 1 0 | 2 0 | 3 1 | 1 0 0 0 0 |
| 17 | 1 1 | 2 1 | 3 2 | 1 0 0 0 1 |
| 18 | 1 2 | 2 2 | 3 3 | 1 0 0 1 0 |
| 19 | 1 3 | 2 3 | 3 4 | 1 0 0 1 1 |
| 20 | 1 4 | 2 4 | 4 0 | 1 0 1 0 0 |
| 21 | 1 5 | 2 5 | 4 1 | 1 0 1 0 1 |
| 22 | 1 6 | 2 6 | 4 2 | 1 0 1 1 0 |
| 23 | 1 7 | 2 7 | 4 3 | 1 0 1 1 1 |
| 24 | 1 8 | 2 8 | 4 4 | 1 1 0 0 0 |
Příklad: 4910 = 25 ( zb. 17 ) 24 ( zb. 1 ) 21 = 1100102
Dekodér
Dekodér je kombinační logický obvod, který ze vstupních dat v určitém kódu vytváří na výstupu jiná, často jednodušší data. Funkce dekodéru je inverzní k funkci kodéru.
Typickým příkladem dekodéru je binární dekodér či demultiplexor, obvod, který binárně kódovaný vstupní signál o n bitech převádí na 2n výstupů, kódovaných jako 1 z 2n. Tak dekodér adresy v paměti počítače převádí část adresy na výstup 1 z n, čímž vybírá např. řádek nebo sloupec paměťové matice.
Jiný běžný typ dekodéru převádí binárně kódovanou číslici na její zobrazení na sedmisegmentovém displeji, čili pro každou vstupní číslici aktivuje příslušné segmenty. Vstup dekodéru bude tedy čtyřbitový (obvykle plus aktivační bit) a výstup by mohl být až 16-bitový, ale pro daný případ stačí sedmibitový. Například je-li na vstupu číslice 8 (IOOO), bude výstup aktivovat všechny segmenty displeje (IIIIIII), kdežto je-li na vstupu 1, bude aktivovat pouze pravé dva.
Složitější dekodér je součástí každého procesoru, kde dekóduje operační znak instrukce (mikroinstrukce), to jest aktivuje příslušná hradla a další signály procesoru k provedení dané instrukce.
Příklad: Dekodér z BCD na 2/5
Kód BCD
Číslicové měřící přístroje zpracovávají desítkové cifry někdy oddělené (rády), je tedy vhodné převést každou cifru na binární tvar zvlášť.
Na číslo do deseti nám postačují 4 binární pozice, tedy 8,4,2,1 (podle řádu). Na rád desítek postačuje 80,40,20,10, pro stovky stačí základní binární pozice násobit stem atd. Toto spojení binárního a desítkového kódování je právě BCD (binary code decimal) kód. Označení BCD(8421) znamená pořadí v kódu, někdy se používá obrácených vah 1248.
Vzhledem k tomu, že existuje šestnáct různých kombinací čtyř bitů, a desítkových číslic je jen deset, je šest kombinací nevyužito. V porovnání s hexadecimální soustavou, kde je pro každé čtyři bity využíváno všech šestnáct hodnot (1010 až 1510 jako písmena AH až FH), je BCD kód z hlediska využití paměti neúsporný.
Že je číslo v BCD kódu, je podstatná a prioritní informace: Bez její znalosti by se totiž bitový zápis mohl jevit jako obyčejné hexadecimální číslo. Z BCD a hexadecimálního kódu vyplývají jiné hodnoty. Například (1001 1001)2 = (99)10 pro BCD kód, ale v hexadecimálním kódování je (1001 1001)2 = (0x99)H = (153)10. Níže je uvede pravdivostní tabulka kódu BCD 8421:
| Číslo10 | A | B | C | D |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
Kód 2z5 (2/5)
Skupina kódů 2/5 patří historicky k nejstarším – kód Industrial 2/5 byl vyvinut firmou Identicon Corporation již v roce 1968. Kód je tvořen znakem Start, znaky 0 až 9 a znakem Stop, je tedy schopen kódovat pouze numerické informace.
Kód je proměnné délky a každý jeho dílčí znak je tvořen pěticí čar, z nichž tři jsou úzké a dva široké. Mezery v tomto kódu nenesou žádnou informaci. Poměr šířky širokého a úzkého elementu je roven 3:1, šířku mezery je doporučeno použít rovnou šířce modulu X.
Kód má velmi široké toleranční pásmo, je tedy vhodný i pro nekvalitní tisk, podklad, špatně přijímající barvu a ztížené podmínky čtení. Nevýhodou je značná délka. Ukázka kódování je v tabulce – 0 odpovídá úzkému, 1 širokému elementu. Kód zvaný Interleaved 2 of 5 (prokládaný 2/5) zakódovává data i do mezer a tím využívá větší prostor čárového kódu pro přenos dat. Díle je uvedena pravdivostní tabulka kódu 2/5.
| 0 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 2 | 0 | 0 | 1 | 0 | 1 |
| 3 | 0 | 0 | 1 | 1 | 0 |
| 4 | 0 | 1 | 0 | 0 | 1 |
| 5 | 0 | 1 | 0 | 1 | 0 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 7 | 1 | 0 | 0 | 0 | 1 |
| 8 | 1 | 0 | 0 | 1 | 0 |
| 9 | 1 | 0 | 1 | 0 | 0 |
Dále uvádím kódování pomocí čar, protože jde o jeden z nějpoužívanějších typů kódů pro lidově zvané čárové kódy.
| Znak | C1 | C2 | C3 | C4 | C5 |
| 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 1 | 0 | 0 | 1 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 1 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 7 | 0 | 0 | 0 | 1 | 1 |
| 8 | 1 | 0 | 0 | 1 | 0 |
| 9 | 0 | 1 | 0 | 1 | 0 |
| Start | 1 | 1 | 0 | – | – |
| Stop | 1 | 0 | 1 | – | – |

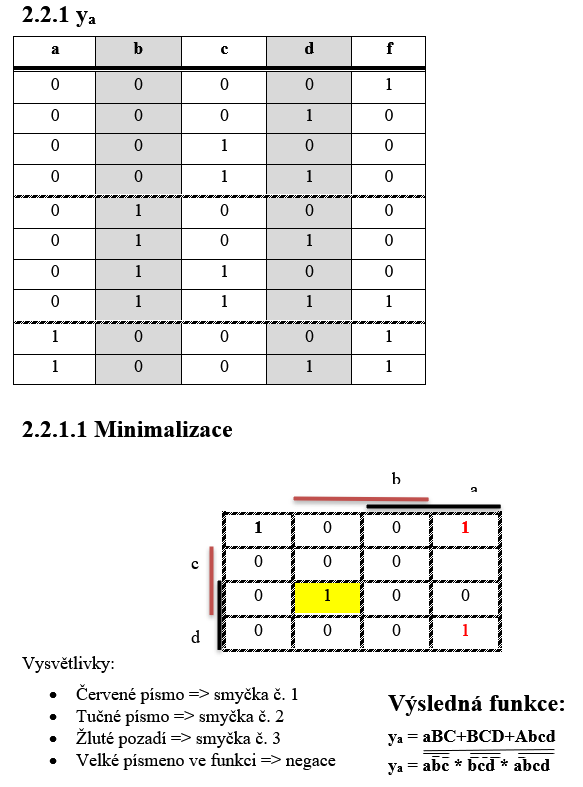
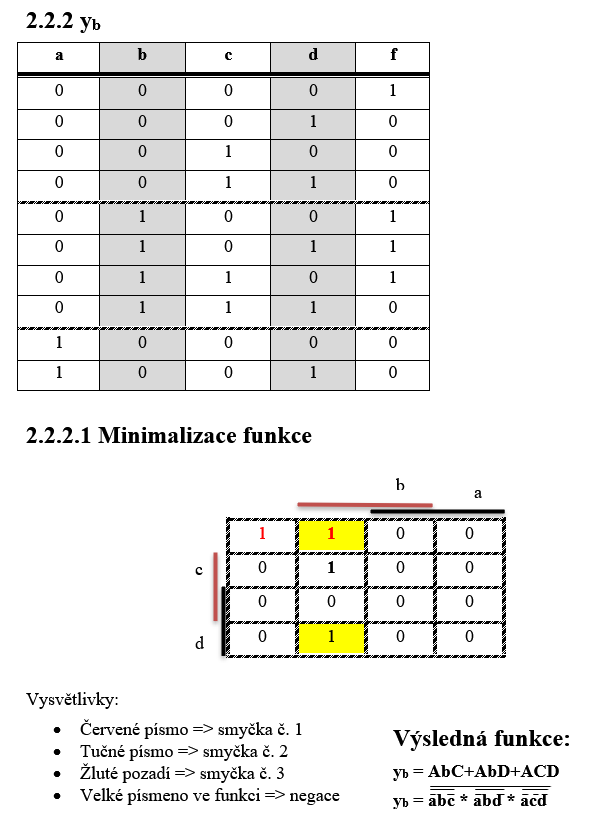
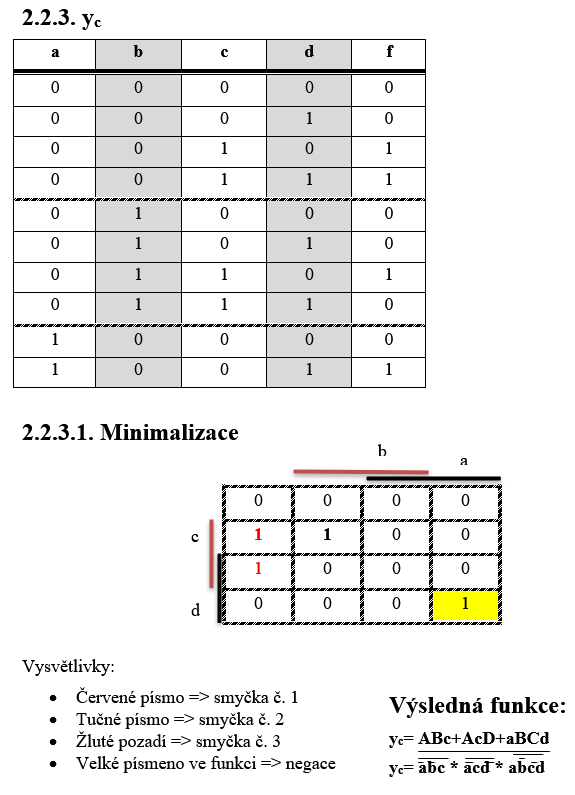
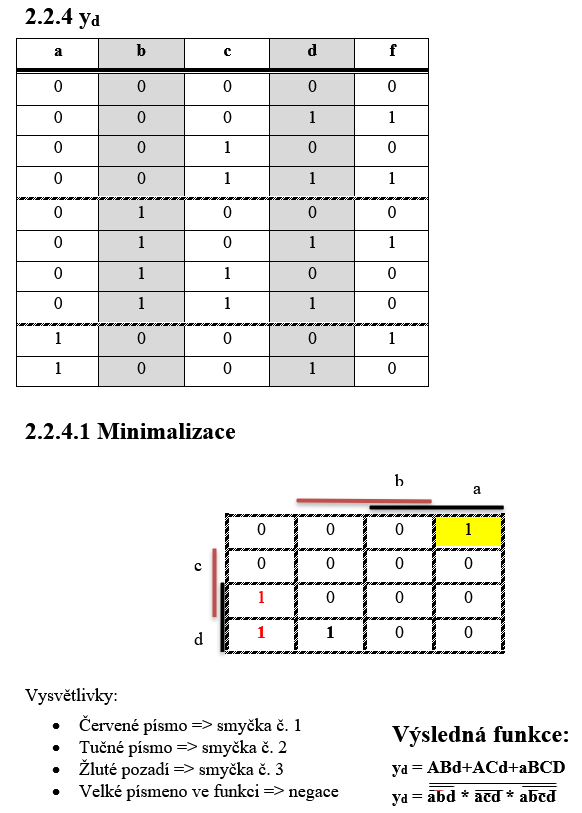
Sestavení funkcí
Funkce budeme sestavovat z kódu 2/5. Jednotlivé nymterny jsou zapsané ve sloupcích, které nesou názvy jednotlivých funkcí.
| funkce | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | číslo |
| Fa(0,7,8,9) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | A |
| Fb(0,4,5,6) | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | B |
| Fc(2,3,6,9) | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | C |
| Fd(1,3,5,8) | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | D |
| Fe(1,2,4,7) | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | E |
Syntéza kódů
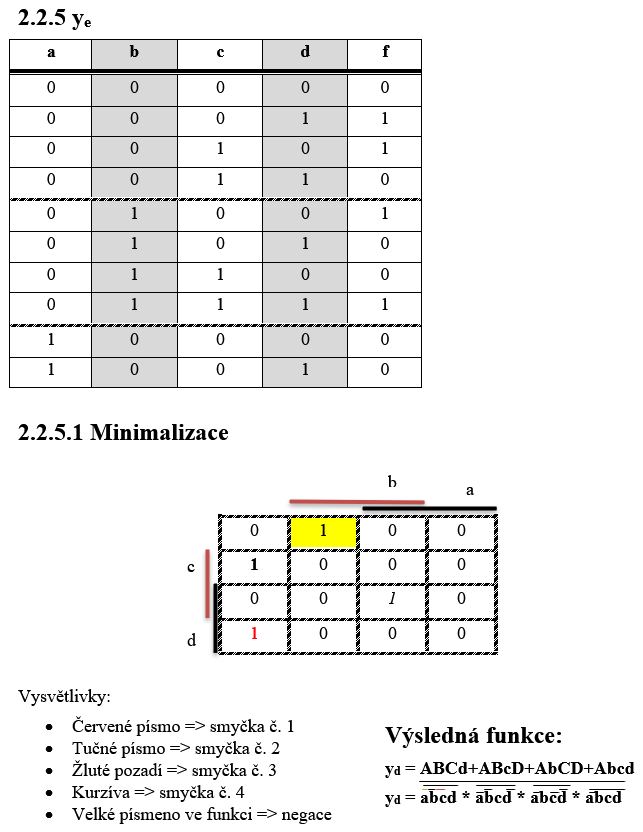
Realizační schéma
| Počet kusů | Součást |
| 5 | Rezistor 220R |
| 5 | LED dioda |
| 5 | MH7410 |
| 5 | MH7420 |
| 1 (6) | MH7404 (dle plošného spoje) |
Grayův kód
Zrcadlový binární kód, známý také jako Grayův kód podle Franka Graye, je binární číselná soustava, ve které se každá dvě po sobě jdoucí čísla liší v jediné číslici.
Zrcadlový binární kód byl původně navržen pro zabránění rušivého výstupu z elektromechanických přepínačů (relé). Dnes je Grayův kód používán pro podporu opravy chyb v digitální komunikaci jako je digitální pozemní televize a některé systémy kabelové televize. Také některé snímače polohy (nebo natočení) udávají polohu v Grayově kódu, aby byl vyloučen výskyt chybné hodnoty při přechodu mezi dvěma sousedními polohami. Grayův kód využívají také odpovídače sekundárního radaru v letadlech.
Důvod vzniku
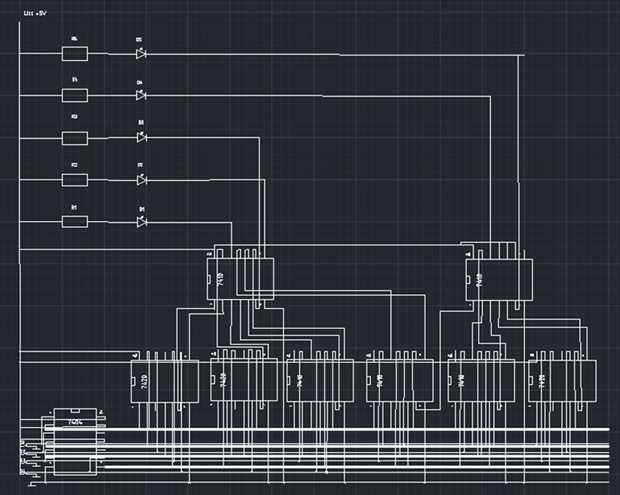
Použití tohoto kódu má význam v elektrických obvodech při čtení hodnoty nesynchronizovaných čítačů (sem spadá i výše zmiňované čidlo polohy). Obecně se problém zajištění „současnosti“ v digitálních systémech řeší pomocí synchronizačního (nebo také hodinového) signálu, avšak v některých případech může být použití synchronizačního signálu nevýhodné.
Při zvýšení hodnoty klasického binárního čítače o jedničku se v mnoha případech mění současně více pozic čítače. Např. při přechodu tříbitového čístače z čísla 3 (binárně 011) na číslo 4 (binárně 100) se současně změní všechny tři pozice. V reálném systému není nikdy možné zaručit, aby se změnilo více logických hodnot naprosto současně, není možné zajistit ani jejich naprosto současné přečtení a vyhodnocení. To znamená, že v případě výše zmíněného tříbitového binárního čítače se může v nepříznivém případě při čtení „na hraně“ stát, že přečteme zcela náhodnou hodnotu od 0 (000) do 7 (111).
Následující příklad znázorňuje graficky čtení bez Grayova kódu.
Ve výše uvedené ukázce by měl obvod plynule přecházet do následujicích stavů:
0000, 0001, 0010, 0011, 0100, 0101, 0110, …
Díky různým zpožděním se v časech t1 až t2 a t3 až t4 dostane obvod do vyznačených stavů:
0000, 0001, (0000), 0010, 0011, 0100, 0101, (0111), 0110, …
Je tak narušen plynulý průběh hodnoty, což může v praxi způsobovat značné nepříjemnosti. Právě tyto přechodové jevy jsou eliminovány použitím Grayova kódu, jak se lze přesvědčit na následujícím obrázku.
Převod na binární kód a naopak
Velmi snadno lze převod do grayova kódu naprogramovat v jazyku C.
unsigned int gray_encode(unsigned int b) {
return b ^ (b >> 1);
} Převod z grayova do binárního kódu vyjde v C-jazyku o něco složitěji:
unsigned int gray_decode( unsigned int g ) {
unsigned int i, b; b = 0; for( i=0; i<8sizeof(g); i++ ) {
b <<= 1; b |= ((b>>1)&0x1) ^ (g>>(8sizeof(g)-1)); g <<= 1;
}
return b;
}Binární zápis kódu
Dvoubitový Grayův kód: 00 01 11 10
Tříbitový Grayův kód: 000 001 011 010 110 111 101 100
Čtyřbitový Grayův kód:
0000 0001 0011 0010 0110 0111 0101 0100 1100 1101 1111 1110 1010 1011 1001 1000
Převody mezi číselnými soustavami
Číselné soustavy používané pro zobrazování v počítači patří mezi soustavy poziční, tj. desítková hodnota každé číslice (znaku) závisí na její pozici vzhledem k řádové čárce.
Váhy v jednotlivých pozicích jsou mocniny základu soustavy.
U desítkové soustavy jsou to mocniny 10
u dvojkové soustavy mocniny 2
u hexadecimální mocniny 16
Desítkové číslo 725 lze tedy rozložit takto:
7*102+2*101+5*100
Podobně postupujeme u čísel vyjádřených ve dvojkové nebo šestnáctkové soustavě, (nebo kterékoliv jiné soustavě) chceme-li zjistit jejich desítkový ekvivalent.
Mocniny základu dvojkové soustavy
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 210 | atd. |
| 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | atd |
Příklady:
Převod z dvojkové do desítkové soustavy
01010111(2) = 1*26 +0*25 +1*24 +0*23 +1*22 +1*21 +1*20 =87(10)
Převod z šestnáctkové do desítkové soustavy
B5(16) = 11*161 +5*160 = 181(10)
U opačných převodů z desítkové soustavy do jiné musíme zjistit, která nejvyšší mocnina základu té soustavy, do níž převádíme, je v desítkovém čísle obsažena, eventuelně kolikrát, jde-li o soustavy s vyšším základem než 2.
Pak je třeba zapsat v příslušné pozici zbytek po odečtení mocniny od převáděného čísla (či po odečtení násobku mocniny)a celý postup opakovat pro výsledek (rozdíl).
Obvykle se používá mechanický postup dělení čísla základem soustavy a zaznamenávání zbytků (u hexadecimální soustavy můžeme dostat možné hodnoty u zbytku 1 – 15, nebo-li 1 – F).
Zbytky zapisujeme od konce, tj. od nejnižšího řádu výsledné převedené hodnoty.
Dílčí výsledky opět dělíme základem soustavy a výsledek posledního dělení je číslice (příp. znak) nejvyššího řádu. Dílčí výsledky opět dělíme základem soustavy a výsledek posledního dělení je číslice (příp. znak) nejvyššího řádu.

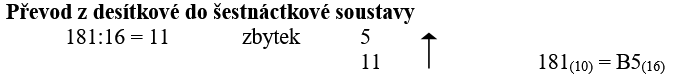
Všimněte si, že pro záznam třímístného desítkového čísla 181 stačí dva hexadecimální znaky, z nichž každý se převede na čtveřici bitů.

Čtveřice bitů (16 kombinací) a jejich odpovídající desítková hodnota (tučně)
dvouciferná čísla nahrazena písmenem , využito v hexadecimální soustavě, 1 čtveřice bitů = 1 šestnáctkový znak, tak se využije všech 16 možností
do 3 bytů, ve kterých je uložena mantisa (při uložení v pohyblivé řádové čárce), se tak „vejde“ větší číslo – až 7 desítkových číslic (=6 hexadecimálních znaků) = tzv. jednoduchá přesnost
písmena představují též desítkovou hodnotu
0000 0 0100 4 1000 8 1100 12 =C
0001 1 0101 5 1001 9 1101 13 =D
0010 2 0110 6 1010 10 =A 1110 14 =E
0011 3 0111 7 1011 11 =B 1111 15 =F